Deskripsi Singkat
Diberikan N titik. Kekuatan dari segmen garis (p_i, p_j) adalah banyaknya segmen garis yang berpotongan dengan segmen garis ini. Carilah kekuatan maksimum dari semua segmen garis.
Link: TLX
Ide
Solusi Naif
Ide: Iterate untuk setiap dua segmen garis, apakah berpotongan?
Kompleksitas waktu: O(N^4)
Solusi
Ide utama: daripada hitung ada berapa banyak yang berpotongan, hitung saja yang tidak berpotongan, lalu eksklusi. Jawaban dari perhitungan = \frac{(N-2)(N-3)}{2} - (\texttt{yang tidak berpotongan})
Untuk tiap segmen garis, hitung ada berapa segmen garis lain sehingga:
- kedua titik berada pada 1 orientasi yang sama (CCW atau CW)
- kedua titik berada pada orientasi yang berbeda, tapi tidak berpotongan
Menghitung kasus 1 itu mudah:
- hitung ada berapa titik pada 1 orientasi (bisa pakai radial sort menggunakan cross product, lalu lakukan binary search)
- hitung banyaknya cara pengambilan 2 titik dari sekumpulan titik
Tapi bagaimana cara menghitung kasus 2? Anggap line segmen sekarang adalah AB dan kita sedang meninjau salah satu titik C yang CCW terhadap vektor \overrightarrow{AB}. Kita ingin mencari titik D sehingga tidak berpotongan dengan segmen AB. Observasinya adalah salah satu kemungkinan titik D pasti CCW terhadap vektor \overrightarrow{AC}.

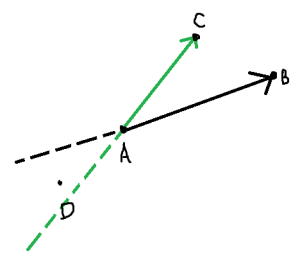
Kalau diperhatikan lebih dalam, jika kita menghitung ada berapa banyak titik yang CCW terhadap vektor \overrightarrow{AC}, kita sudah menghitung kasus 1 dan kasus 2 secara bersamaan untuk orientasi CCW.
Untuk menghitung orientasi yang lain, kita hitung menggunakan vektor \overrightarrow{BA} menggunakan cara yang sama. Definisikan f(\overrightarrow{AB}) sebagai banyaknya titik D sehingga \overrightarrow{AD} CCW terhadap \overrightarrow{AC} untuk setiap \overrightarrow{AC} yang CCW terhadap \overrightarrow{AB}. Dengan begitu, jawabannya = \frac{(N-2)(N-3)}{2} - f(\overrightarrow{AB}) - f(\overrightarrow{BA}).
Kalau kita lakukan ini secara naif akan seperti begini. Untuk setiap vektor \overrightarrow{AB} lakukan radial sort semua vector \overrightarrow{AC}. Hitung ada berapa \overrightarrow{AC} yang CCW. Anggap nilai ini adalah g(\overrightarrow{AB}).
Kemudian, nilai f(\overrightarrow{AB}) adalah penjumlahan dari g(\overrightarrow{AC}) sehingga \overrightarrow{AC} itu CCW terhadap \overrightarrow{AB}. Artinya kita tinggal iterate aja.
Dapat kompleksitas waktu O(N^2 \times N \log N) = O(N^3 \log N). Sayangnya masih TLE.
Kita bisa percepat perhitungan g(\overrightarrow{AB}). Daripada kita iterate untuk setiap vektor, kita bisa iterate untuk setiap titik A. Kok bisa? Perhatikan bahwa relative ordering dari vektor setelah melakukan radial sort itu tetap sama kalau berasal dari source yang sama.

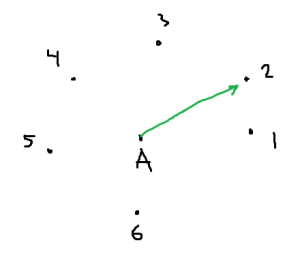
Dengan ini, kita bisa percepat perhitungan g menjadi O(N^2 \log N). Selain itu, nilai f juga bisa dihitung dengan cepat karena kita bisa menggunakan two pointers saja. Observasinya adalah vektor-vektor yang CCW selalu bergerombolan, dan tiap kali kita pindah ke vektor acuan \overrightarrow{AB'} selanjutnya, range yang kita pantau hanya akan bergerak ke indeks selanjutnya juga. Dengan begitu, perhitungan f akan memerlukan kompleksitas waktu O(N^2).
Total kompleksitas waktu: O(N^2 \log N)
Catatan Akhir
Kalau mau memahami lebih dalam tentang cross product (vektor secara general), aku saranin untuk coba kerja soal ini dan coba implementasi. Ada banyak cara untuk mengimplementasikan solusi ini. Jadi, cari cara yang nyaman untuk implementasiin ide ini.